ACTING PHYSICS

MATHEMATICS

The sculpture and the music are based on the same mathematical probability distribution -

the Poisson distribution

named after the French mathematician Simeon Dénis Poisson (1781 - 1840).

For things interacting at random, like cars on a street or muons from space, the Poisson distribution can be used to compute the probability for how often these things will appear during a certain pre-determined time interval.
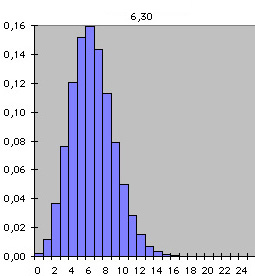
From where we stand, what is the probability of observing exactly one passing car during a one-minute interval? None at all? Exactly two? And so on . . . It turns out that muons and passing cars (and many other phenomena) follow the same type of probability distribution, the Poisson distribution.

  The conditions that give rise to the Poisson distribution can be described in the following way: The number of cars (muons) is very large. Each one of these has a precise, small, probability to pass exactly the place where we stand ready to count them. What we observe is thus the compound effect of a very large number of random occurrences, which each has a small probability to "succeed" i.e. pass where we stand and count them.
Imagine for example that we count the number of persons that pass during a given interval, e.g. one minute. This will give an integer. If we repeat this procedure a large number of times we will obtain a sequence of integers. If we make a plot in a diagram showing how often each digit appears we will obtain a Poisson distribution. The plot shows the probability that three or ten persons will pass in the period of one minute. If you divide the number of persons with the number of time-intervals you have counted, you obtain the average number of persons in one minute. The average does not have to be an integer, even though the number of persons you count always is. If, for example, you count seven persons in a two minute period the average is three and a half.
The Poisson distributions representing different averages have different shapes. Two of the towers in the sculpture are direct representations of Poisson distributions.