MATEMATIK
Skulpturens torn och musiken är skapade utifrån samma matematiska sannolikhetsfördelning
matematik musik fysik program 2000 i februari
Poissonfördelning
sannolikheten efter den franske matematikern Simeon Dénis Poisson 1781-1840.
Om något passerar slumpmässigt, som bilar på en väg eller myoner från rymden, så kan man försöka beskriva förloppet genom att ange sannolikheterna för att observera olika antal händelser under säg en minut.
|

|
Låt säga att vi bestämmer oss för att räkna hur många personer som passerar förbi under en bestämd tid t ex en minut. Vi får då ett heltal. Gör vi om samma procedur, dvs räknar antal personer under en minut, tillräckligt många gånger får vi en serie av heltal.
|
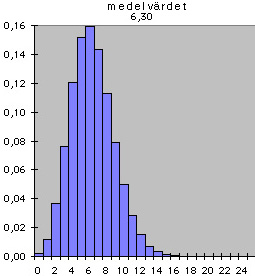 antal per tidsenhet
antal per tidsenhet